(057-41) 5-23-18

Шкільна математична олімпіада 6 - 7 класи

 

1 тур(2 години)

 

Частина перша

 

Вказати тільки одну правильну відповідь.

1. Квиток у кінотеатр коштує 11 грн, диск улюбленої групи - 20 грн, чіпси - 3,5 грн, проїзд на маршрутному таксі - 0,75 грн. Антон має 32 грн. Скільки з наведених тверджень не є пра­вильними? 1) Антонові не вистачить грошей на диск, кіно і чіпси. 2)Після купівлі диска і відвідування кіноте­атру в Антона залишаться гроші на проїзд у мар­шрутному таксі. 3)Поїздка в маршрутному таксі і купівля чіпсів не дозволять Антонові придбати два квитки в кінотеатр.

всі наступні пункти хибні;
усі не вірні;
усі вірні;
2 правильних і 1 неправильне.

2. Токарі Василь, Микола, Петро, Сергій повинні за два дні виготовити 42,18,24,37 деталей відповідно. Двоє з них виконали завдан­ня в перший день, третій хворів перший день, він усе своє завдання виконав за другий день, а четвертий обидва дні хворів, але загальне зав­дання двох днів було виконано повністю. Хто з токарів хворів, якщо токарі, які працювали у перший день, другого дня зробили стільки, скільки й першого?

хворів Микола;
хворів Василь;
хворів Сергій;
всі попередні пункти хибні.

3. Батьки маленького Сергійка мають вико­нати три види домашньої роботи: 1)почистити килими (на це потрібно 40 хв, вони мають 1 пилосос); 2)підрізати дерева в саду (на це потрібно 40 хв, у них є одні ножиці); 3)нагодувати й заколисати Сергійка (на це потрібно 40 хв). Кожну з цих робіт може виконувати кожен з батьків. Як розподілити цю роботу між батька­ми, щоб закінчити її в найкоротший час?

60 хв.;
50 хв.;
40 хв;
всі попередні пункти хибні.

4. Лічильник автомобіля показував 23 932 км. Через 3 год на лічильнику знову з'явилося число, що однаково читається з обох кінців. З якою швидкістю їхав автомобіль? Швидкість вира­жається цілим числом.

65 км/год;
60 км/год;
70 км/год;
всі попередні пункти не вірні.

5. 15 кульок можна скласти у вигляді три­кутника, але не можна у вигляді квадрата - однієї кулі не вистачає. З якої кількості кульок, мен­шої від 50, можна скласти як трикутник, так і квадрат?

з 25 кульок;
з 49 кульок;
з 36 кульок;
всі попередні пункти не вірні.

6. Дати часто записують так: число, місяць, дві останні цифри року, наприклад, 9.5.05 – де­в'ятого травня 1905 р. Скільки разів протягом XX століття дату можна було записати, викори­стовуючи тільки одну цифру?

12;
14;
13;
всі попередні пункти не вірні.

7. Учні вирішили поїхати в цирк на автобусі. Замовлення автобуса коштує 100 грн, а квиток у цирк на одного – 5 грн. Вирішили, що кожен учень внесе по 8 грн. Яка найменша кількість учасників має взяти участь у поїздці, щоб мож­на було покрити усі витрати?

34 учні;
32 учні;
33 учні;
всі попередні пункти не вірні.

8. Батьки придбали люстру з 15 лампочками і хочуть мати можливість вмикати будь-яку кількість із них від 1 до 15 – одну, чи дві, чи три, чи .... Яка найменша кількість звичайних вимикачів знадобиться для цього?

6 лампочок;
8 лампочок;
7 лампочок.;
всі попередні пункти хибні.

9. Скількома способами шість шахістів, серед яких є два майстри спорту, можуть об'єднатися у дві команди по 3 спортсмени в кожній для одночасної гри в двох містах так, щоб у кожній команді був майстер спорту?

15;
13;
12;
всі попередні пункти хибні.

10. У супермаркеті два ескалатори: один піднімає клієнтів вгору, другий спускає їх униз. Одна особа біжить по ескалатору, що їде вгору, і в результаті піднімається зі швидкістю 2,5 м/с. Друга особа з тією самою швидкістю біжить угору по ескалатору, що спускається вниз, і в резуль­таті піднімається вгору зі швидкістю 0,5 м/с. З якою швидкістю рухаються ескалатори, якщо ці швидкості однакові?

0,9;
1,2;
0,25;
1.

11. Учаснику олімпіади відразу нараховуєть­ся 100 балів. За кожну правильно розв'язану задачу набрана до цього моменту кількість балів збільшується на 10 %, а за неправильно розв'я­зану задачу — зменшується на 10 %. Після розв'язання кількох задач в учасника олімпіади ви­явилося 80,19 бала. Скільки при цьому задач він розв'язав правильно?

1;
2;
3;
всі попередні пункти хибні.

12. У класі 30 учнів. Вони здавали залік з математики по черзі. Перший одержав 10 балів, другий — 8 балів, а кожен наступний одержав кількість балів, яка дорівнює середньому арифметичному кількостей всіх балів, отриманих попередніми учнями. Яку оцінку одержав останній учень?

всі наступні пункти хибні;
12;
9;
10.

 

ЧАСТИНА ДРУГА

 

Записати повне розв’язання задач  і записати відповідь.

 

1. Шість однакових діжок вміщують 28 відер води. Скільки відер води можуть вмістити таких 15 діжок?

 

2. Дмитро і Максим грають у таку гру. За свій хід гравець повинен за декілька пострілів і попасти в деякі області мішені(див. рис.), так щоб сума вибитих очок

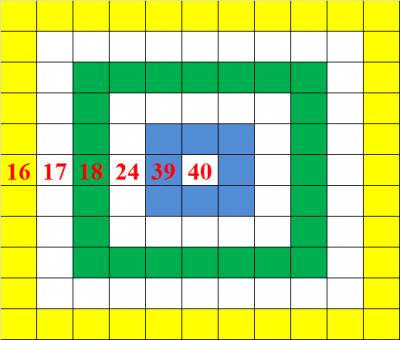
дорівнювала 80, при цьому 80 очок треба вибити іншим способом. Виграє той, хто останнім виб’є потрібну суму очок. Хто з гравців забезпечить собі перемогу, якщо гру розпочинає Дмитро? Детально обґрунтуйте відповідь.

 

3. Запиши сотню дев’ятьма різними числами від 1 до 9, які записані у порядку зростання та з’єднані знаками арифметичних дій.  Скількома способами число 100 можна так записати? 

 

4. Поясни, чому 9999¹⁰ більше, ніж  99²⁰?

 

5. Є двоє пісочних годинників: на 7 хвилин і на 11 хвилин. Куряче яйце вариться 15 хвилин. Як відміряти цей час за допомогою наявних годинників?

 

6. За один хід число, написане на дошці, дозволяється або замінити на подвоєне, або стерти в нього останню цифру. Спочатку на дошці написано число 458. Як за декілька ходів отримати число 14?

 

 

 

 

 

Відповіді до задач першого туру

 

Перша частина.

1. 2 правильних і 1 неправильне;

2. хворів Василь;

3. 60 хв.;

4. 70 км/год;

5. з 36 кульок;

6. 13;

7. 34 учні;

8. 8 лампочок;

9. 12;

10. 1;

11. 1;

12. 9.

Друга частина.

1.     Розв’язання. 28:2=14 відер вміщують три діжки(6:2=3).

                       14·5=70 відер води вміщують 15 діжок(3·5=15).

Відповідь: 70 діжок.

2.Розв’язання. Всього п’ять різних способів за один хід набрати рівно 80 очок.

Ось вони: 16*5=80,

                 40*2=80,

                 23+17+40=80,

                 16+24+40=80,

                 2*24+2*16=80.

Таким чином,  забезпечить собі перемогу починаючий, так як він робить п’ятий  непарний хід. А це за умовою задачі Дмитро.

3.Розв’язання.

1.     1+2+3+4+5+6+7+8*9=100;

2.     12-3-4+5-6+7+89=100;

3.     123+45-67+8-9=100;

4.     123-4-5-6-7+8- 9=100;

5.     123-45-67+89=100;

6.     123+4-5+67-89=100;

7.     12+3-4+5+67+8+9=100; … і так далі.

 

     4. Розв’язання. 

         9999¹⁰  = [99 (100+1)] ¹⁰  = 99¹⁰ 101 ¹⁰ > 99¹⁰ 99¹⁰  =  99²⁰?